Photo by Nic Rosenau on UnsplashSo, you're studying trigonometry and the teacher tells you to convert radians to degrees.
You wonder, "How do I do that?" Better still, you wonder what a radian is and why it even matters.
Let me show you how to convert radians to degrees. It's essential to working with circles!
What Is a Radian?
Before you convert radians to degrees, you should be comfortable measuring angles in degrees and remember that a full circle is 360 degrees.
Radians take a different approach — they measure angles using the circle’s radius.
A radius is the distance from the center to the circumference of a circle — half of the circle's diameter.
GIF created by Wendy F. McMillian
Picture this: take the radius of a circle, lay it along the circle’s edge to create an arc, then draw a line from the arc back to the center. That’s one radian! Radians are directly related to the radius of a circle — this is why they're important!
Radians are a more accurate method for measuring circles, making higher maths easier to solve.
GIF created by Wendy F. McMillian
Think of it like this:
You already know the formula for the circumference of a circle is 2 × π × radius.
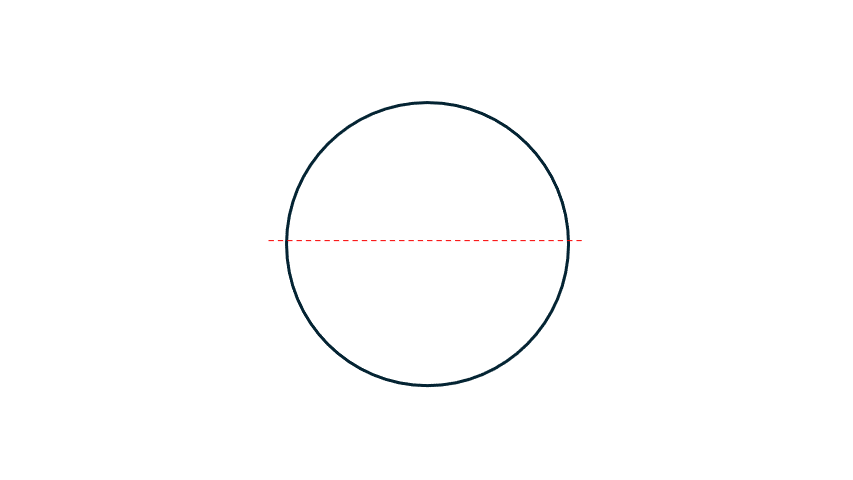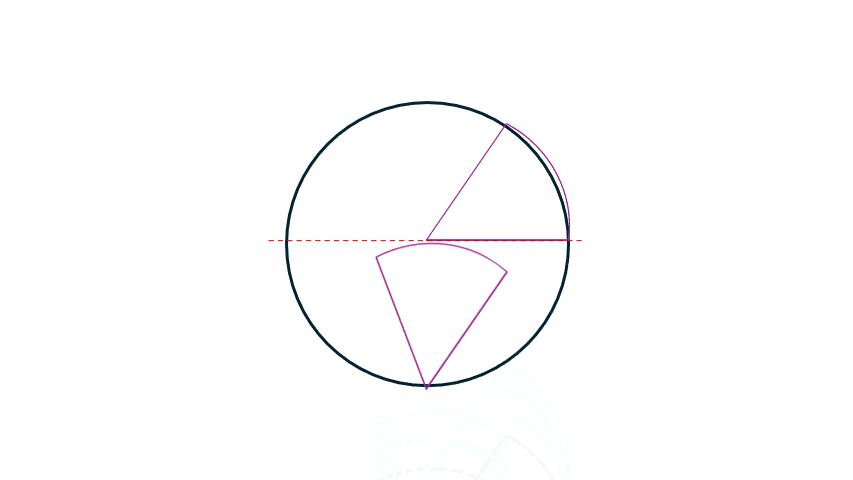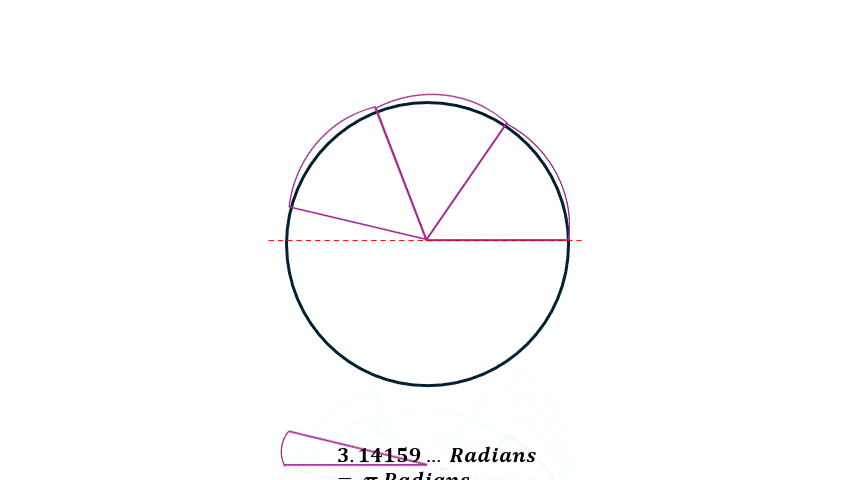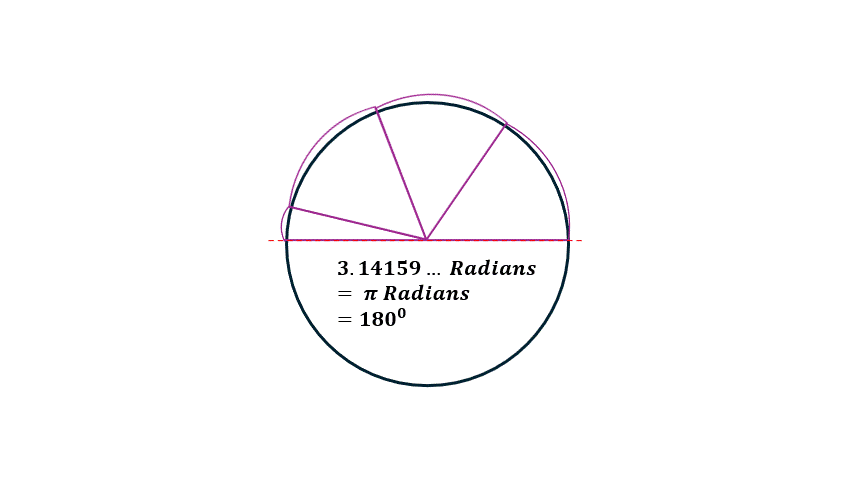
Now, in a unit circle with a radius of 1, that formula becomes just 2π (half that distance is just π).
But here’s the cool part: in radians, 2π isn’t just the distance around the circle, it’s the total angle measure of the circle too!
So, if you take an arc the same length as the radius, you’ve got 1 radian.
Go around the circle and — boom — you’ve traveled 2π radians.
It’s math magic…well, math logic, but magic sounds cooler! 🪄
Radians and Degrees, Oh My!
Radians, like degrees, are just another way to measure angles.
Since the circumference of a circle is found using 2 × π × radius, and a full circle measures 360 degrees, the two systems are connected. A complete circle measures 2π radians, which is the same as 360 degrees.
Figuring out how to convert radians to degrees is a key step in trigonometry. Degrees and radians are like two languages that say the same thing — you just need the right translation. A half circle is 180 degrees, which equals π radians (or a straight line).
Cut that in half again, and you’ve got 90 degrees, or π/2 radians — better known as a right angle. Easy, right?
It’s like slicing pizza, first in half, then in quarters…except here you’re serving up math instead of pepperoni!
Convert Radians to Degrees in One Step
It's easy to convert radians to degrees and vice versa when you know the formula or the ratio that converts between the two.
That formula to convert radians to degrees is:
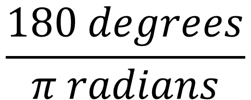Image created by Wendy F. McMillian
Remember that 180 degrees (half a circle) equals 3.14159...radians or π radians.
Say you have a measure of 5π/4 radians to convert to degrees. Using the ratio above, you can easily convert them!
Image created by Wendy F. McMillian
Image created by Wendy F. McMillian
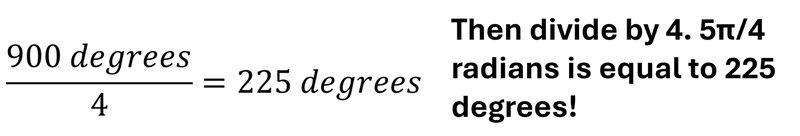Image created by Wendy F. McMillian
What if you're given 60 degrees and need to convert to radians? Just flip the formula!
Image created by Wendy F. McMillian
Image created by Wendy F. McMillian
Quiz
You’ve decided to cut that pizza into 8 equal pieces. At what angle should each piece be cut?
Radians to Memorize
Below is an image of a radian circle (or unit circle), which lists the most popular radians and their degrees. You can use it as a quick reference chart to convert radians to degrees.
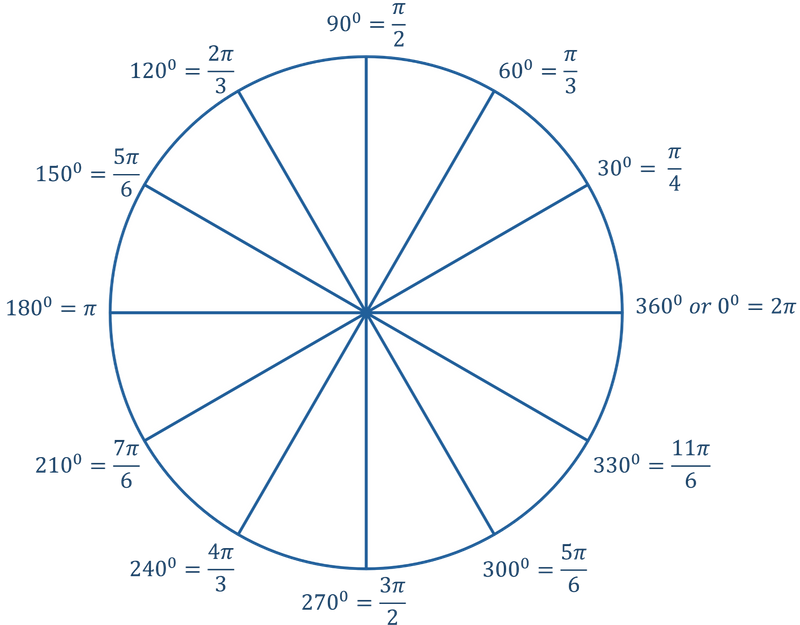Image created by Wendy F. McMillian (to hear an audio description of the image, press play on the audio player below)
When working with radians, degrees, and circles, you should familiarize yourself with some well-known measures — like the ones above.
Knowing these measures will speed up your higher math calculations even more!
Take Action
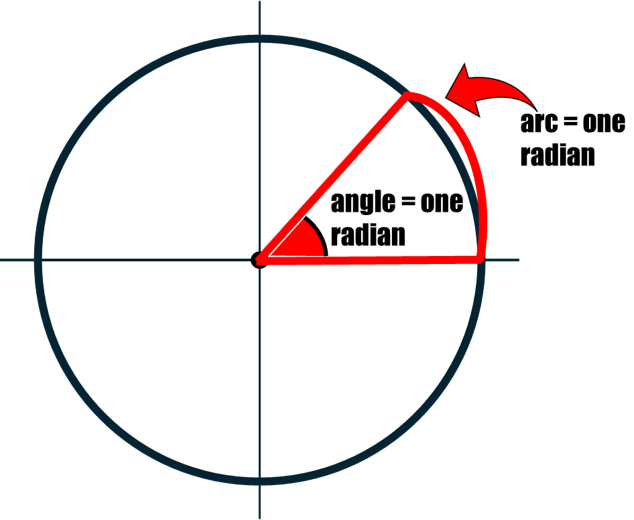Image created by Wendy F. McMillian
Now, it's your turn!
You should easily be able to convert radians to degrees and back again.
But if you need more help or something isn't clicking, check out these sites:
Your feedback matters to us.
This Byte helped me better understand the topic.